In order to see how changes in ocean heat
transport impact the evolution of SST anomalies we integrated the
Lamont ocean GCM (Visbeck et al. 1998), coupled to the AML model, for the 1958-1998 period forced
by the NCEP reanalyzed wind stresses as well as the wind speed and
direction that are used within the AML. The GCM spans the Atlantic
Ocean from
![]() to
to
![]() with a resolution of
with a resolution of
![]() by
by ![]() ,
and 30 fixed vertical levels, 13 of which
are in the upper 1000m. The model includes basin geometry and
bathymetry consistent with the resolution. Temperature and salinity
are restored to climatology at the northern and southern boundaries.
The model includes a simple one and a half layer thermodynamic sea ice
model, a bulk wind-driven mixed layer model, convective adjustment and
isopycnal thickness diffusion. The mixed layer depth is now computed
and can deviate from its climatological values.
,
and 30 fixed vertical levels, 13 of which
are in the upper 1000m. The model includes basin geometry and
bathymetry consistent with the resolution. Temperature and salinity
are restored to climatology at the northern and southern boundaries.
The model includes a simple one and a half layer thermodynamic sea ice
model, a bulk wind-driven mixed layer model, convective adjustment and
isopycnal thickness diffusion. The mixed layer depth is now computed
and can deviate from its climatological values.
When the model is forced with the total (climatology plus anomaly) forcing fields from the NCEP reanalyses it produces quite substantial errors in SST which is in contrast to the model simulations using other forcing products (e.g. European Center for Medium Range Weather Forecasts analyses). While the anomalies around this incorrect mean are quite realistic we attempt to avoid potential problems by applying instead a correction in the form of a diagnosed seasonally varying mean flux that ensures the model reproduces a reasonable mean seasonal cycle of SST. The equation for the GCM's SST, T, can be written schematically as:
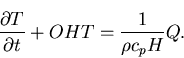 |
(7) |
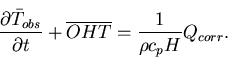 |
(8) |
![\begin{displaymath}\frac{\partial T}{\partial t} + \overline{OHT} +OHT' =
\frac{...
...r}
+\left[Q(\bar{T}_{obs}+T')-Q(\bar{T}_{obs})\right] \right).
\end{displaymath}](img41.gif) |
(9) |
![\begin{displaymath}\frac{\partial T'}{\partial t} + OHT' = \frac{1}{\rho c_pH}\left[Q(\bar{T}_{obs}+T')-Q(\bar{T}_{obs})\right],
\end{displaymath}](img42.gif) |
(10) |
Figure 7b shows the winds and modeled
SST anomaly corresponding to the first
mode of modeled SST variability in the GCM. Figure 7c shows the
corresponding time series. It is immediately apparent that the
pattern is very similar to both the pattern derived by the ocean mixed
layer models and to the observations. There are however a few
differences. The GCM now more faithfully reproduces the magnitude of
the SST anomalies in the far North Atlantic which were overestimated
by the uniform depth ocean mixed layer model and underestimated by the
variable depth model. It is also apparent that the GCM faithfully
reproduces the warm SST anomalies that occur south of the North
Atlantic Current between
![]() and
and
![]() .
.
To compare the roles of surface fluxes and ocean heat transport in determining the SST variability we performed two regressions of the modeled surface heat fluxes and anomalous ocean heat transports, integrated down to the base of the modeled ocean mixed layer, each against the time series of the SST anomalies of the first SVD mode. These are shown in Fig 8a and 8b. The anomalous ocean heat transport is defined positive if it warms the SST whereas the anomalous surface heat flux is positive if it cools the SST. The surface heat fluxes perfectly match the SST anomalies in the sense of the atmosphere forcing the ocean. Ocean heat transport is important in the northern North Atlantic where it is the same magnitude as the surface fluxes. We broke the anomalous heat transport into two terms, advection of the mean SSTs by the anomalous currents and advection of the anomalous SSTs by the mean currents. Advection of the mean temperature by the anomalous currents was the most important term throughout the basin. During a high index NAO year, stronger westerlies drive a southward Ekman drift over the high-latitude ocean that cools the SSTs. This amplifies the cooling due to enhanced surface fluxes. This anomalous Ekman drift increases the simulated SST anomalies relative to the case with a variable depth mixed layer. Clearly, the reasonably sized SST anomalies simulated with a uniform mixed layer depth, and no anomalous ocean heat transport, were obtained for the wrong reason. In reality, mixing down to considerable depths, ocean heat transport and surface fluxes are important in this area.
Further south, stronger trades drive a northward Ekman drift that warms the subtropics and southern mid-latitudes. This weakly opposes the cooling of the subtropics by surface fluxes but enhances the warming to the south of the North Atlantic Drift. In the latter region this causes a warming in the GCM which is realistic, but was missed by the ocean mixed layer models. The strong anomalies seen in the data in the region of the North Atlantic Current region are not reproduced by the mixed layer model or the GCM. The GCM's Gulf Stream and North Atlantic Current are located too far north and lead to increased SST variability in the region east of Canada. It is probable that ocean heat transport is responsible for some of the observed variability of SST in the North Atlantic Current region but this low resolution GCM cannot capture this. The GCM also has an improved SST simulation in the Gulf of Guinea which may indicate a role for equatorial dynamics.
To further examine the role of ocean heat transport we looked at the heat budget of the ocean mixed layer averaged over different areas. First we took an areal average over the subtropical North Atlantic. Here the time series (not shown) of the heat budget terms show strong correspondence between changes in SST, the surface fluxes and the wind forcing but no systematic relationship to the ocean heat transport. This suggests that the weak relationship between SST and ocean heat transport uncovered by the SVD analysis is of marginal statistical significance. In contrast, an area average in the subpolar gyre shows a strong relationship between SST changes, surface fluxes, ocean heat transport and the wind forcing. Increased westerlies cause dynamical cooling of the ocean that is in phase with the cooling by surface fluxes. This is further evidence for our claim that changes in ocean heat transport are primarily associated with anomalous Ekman drifts that establish themselves instantaneously once the wind changes. We also computed the time series of northward heat flux by the Gulf Stream off Cape Hatteras. This showed no decadal variability or trend in contrast with the coupled model runs of Grötzner et al. (1998) where heat transport in this area precedes the development of SST anomalies in the subpolar gyre. We were unable to find any evidence for any lead or lag relationship involving ocean heat transports. While this is not a comprehensive examination of the possible roles for ocean heat transport it is in contrast with model simulations of the tropical Pacific Ocean where it easy to identify changes in ocean heat transport leading the development of SST anomalies (e.g. Seager 1989).
As a final assessment of the model's ability to reproduce the dominant mode of observed climate variability we show in Fig 9 the modeled SST anomalies for January-February-March averages of 1969 and 1989. These can be compared with the observed SST anomalies for that period shown in Figure 2. It is quite clear that, with modest differences in position and amplitude, the GCM can accurately reproduce the observed variability.
We also examined the higher modes of observed and modeled
variability. The second and third modes together explain less
variance of SST than the first mode alone. Both higher modes are high
latitude features dominated by anomalous circulations at around
![]() ,
that associated with the third mode being located much
further east than that associated with the second mode. Both modes
are dominated by interannual variability without any noticeable
trend. The ocean GCM reasonably reproduces the patterns and time
evolution of these modes. We regressed the ocean heat transport and
surface fluxes onto the time series of the pattern of modeled SST
revealed by the SVD analyses. For the second mode anomalous surface heat fluxes are the dominant forcing
for SST variability with changes in ocean heat transport contributing
in the North Atlantic Current region at about
,
that associated with the third mode being located much
further east than that associated with the second mode. Both modes
are dominated by interannual variability without any noticeable
trend. The ocean GCM reasonably reproduces the patterns and time
evolution of these modes. We regressed the ocean heat transport and
surface fluxes onto the time series of the pattern of modeled SST
revealed by the SVD analyses. For the second mode anomalous surface heat fluxes are the dominant forcing
for SST variability with changes in ocean heat transport contributing
in the North Atlantic Current region at about
![]() .
Patterns
of surface fluxes, ocean heat trasnport and SST are not coherently
linked for the third mode which makes us wonder about it's realism and
we do not consider it further.
.
Patterns
of surface fluxes, ocean heat trasnport and SST are not coherently
linked for the third mode which makes us wonder about it's realism and
we do not consider it further.